THREE FORCE PRINCIPLE

If a body in equilibrium has three forces, they must be concurrent.

Type	Video Lesson Description and Link	Duration	Date
Lecture	Lecture: Three Force Principle
Online	Worked question: Pole with cables		20200427
Online	Worked question: Counterbalanced loader crane	5:09	20200504

Why three forces must be concurrent.

To ensure equilibrium, there can be no rotation. This can only be achieved if all three forces intersect at one point. On top of that, the forces must add up to give zero resultant.

Steps in a typical Three Force problem

Steps in the 3 Force Principle (For some typical questions)
1. Isolate the body in question.
2. Locate the points on the body where the 3 forces are applied. (Usually where it touches, gravity through the centre)
3. Determine as many force direction as possible. (Often 2 of the forces have known direction such as gravity (270 degrees), roller force (perpendicular to surface), cable force (along centreline of cable) etc.
4. Locate the intersection, then determine the angle of the 3rd force. (Since it must also go through the same intersection point. You should now have all three angles.
5. Now draw the force polygon.

Remember.

The point of intersection can be arbitrary (random) - it is not always a joint or a location WHERE forces are applied. It is often out in space somewhere away from the body.
Make sure you keep the diagrams separate; Space Diagram, FBD and FPolygon. This is very important in these questions because an accurate Picture (Space Diagram) is needed in order to obtain the point of intersection and correct force angles.

In many cases, the point of intersection is arbitrary. It may not even be on the body.

Diagrams

The Space Diagram (SD)

It is usually necessary to sketch accurately, showing dimensions. This must be a scaled drawing.

The Free Body Diagram (FBD)

Since forces are concurrent, the Free Body Diagram is a dot, but we still need a SD to determine angles (see step 3 below). See Free Body Diagrams for more information.

Isolate the body.
Locate contact points (border crossings). There should be three of course
Line of Action. Back in the Space Diagram, determine the line-of-action of forces using the rules for standard connections (support reactions). Now find the single point of intersection for the three forces. This will give all the angles.
"To the Body". Identify the direction as applied "to the body".

The Force Polygon (FP)

The force polygon must be drawn strictly to scale, and everything is a Force. The only information coming from the FBD is; Force magnitudes and Force Angles.
Since there are three forces, we should have a force triangle. Assuming we know all angles and have unknown lengths this can be solved using CAD, or geometrically using the sine rule. Using the components method you should end up with simultaneous equations which can be solved by substitution.

STEP BY STEP...
The Sketch (Space diagram)
1. Identify a body with 3 relevant forces.
2. Get all the information you can. Especially ANGLES. Look for gravity (270^o), special reactions like cables (Angle=cable angle & tensile), no friction (90^o to surface) etc. See table below. (Support Reactions)
3. You must know the direction of 2 forces. Where these intersect is the concurrency point. The third force (unknown angle) must also go through this point.
4. If you drew the relevant details to scale, you now have ALL 3 ANGLES. You have finished the sketch.
The FBD
1. The FBD is now a dot (treated as a concurrent force problem).
2. Ensure all forces are in 360 notation

------------------------ ONLY ANGLES ALLOWED PAST THIS POINT ----------------------

The FP
1. Make sure you only copy ANGLES from the FBD. Nothing else!
2. You must know magnitude of at least 1 force (common), maybe 2.

Support Reactions

You will need to determine the angle of some forces in order to find the intersection point.

From Vector Mechanics for Engineers: Beer, Johnston, Eisenberg, Staab p165

Worked Example 1

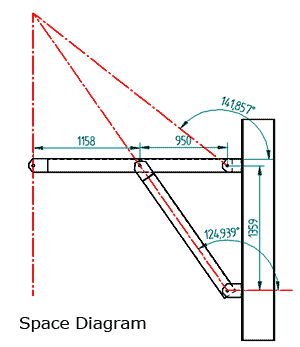
Braced Frame A weight force of 150kN hangs from the end of this beam. The beam is supported by a strut. Note: The strut is a 2 force body The beam is a 3 force body
Scale Drawing (Space Diagram) Draw this diagram accurately to scale. We need to pick a body with three forces (the beam).
Determine intersection point from the Scale Drawing (Space Diagram) What we know: The gravity force is vertical The strut force must be in line with joints Therfore we obtain the intersection of these 2 forces, and hence the thiird force must go through the same point. Now we know the angle of the 3rd force that goes through the pin joint between the wall and the beam. (pin joints can have force at any angle)
The FBD We know all three angles (from the above space diagram). There are 2 unknown magnitudes
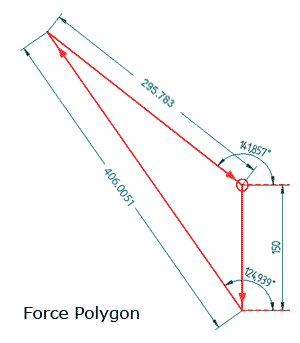
The Force Polygon Start with the 150kN vertical force at 270^o. Now add an unknown length line at 124.939^o The last unknown length line at 141.857^o must get back to the start point, so draw it attached to the start. Now trim these unknown length line together to give the completed Force Triangle. Dimension to get Forces.
Autocad sample file: strut-example.dwg or strut-example.zip Note: The answer 406.0051kN is based on the vertical length of 1360mm.

Worked Example 2

Lifting a pole

A man pulls on a rope to raises a 10 kg pole, of length 4m. Find the tension in the rope and the reaction at A.

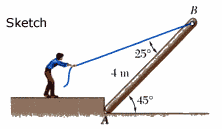FBD to Scale.

The body with 3 forces is the log.
We know direction of gravity at G.
We know direction of cable force at B.
Draw this diagram accurately to scale to get intersection point of these 2 forces, and hence the angle of the 3rd force at A.

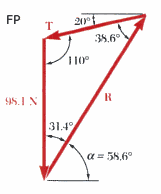
Force Polygon

Start with the 95.1N vertical force at 270^o.
Now add an unknown length line at 58.6^o
The last unknown length line at 200^o must get back to the start point, so draw it attached to the start.
Now trim these unknown length line together to give the completed Force Triangle.
Dimension to get Forces.

Above illustrations from Vector Mechanics for Engineers: Statics. 7th ed. Beer, Johnston, Eisenberg, Staab. McGraw Hill. 2005 (GoogleBooks)

Summary: Equilibrium of Concurrent Forces

So far we have only discussed forces that intersect at one common point (concurrent forces). Sometimes this is not obvious - especially in the case of three forces. For equilibrium of concurrent forces, we must check two things:

Do the forces intersect at one point? (Concurrent)
Does the Force Polygon add up to zero resultant (closed loop)?

Number of forces	FBD (Line of action plan)	Force Polygon (Magnitude plan)
2	Forces must be collinear. Cables, struts, pin jointed members with 2 connections.	Forces must be "on top of each other" and in opposite directions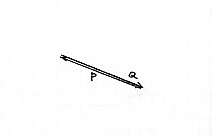
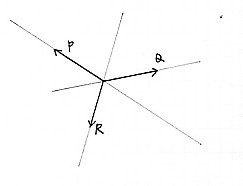
3	Forces must intersect at one point.	Forces must form a closed triangle
4	Forces must intersect at one point	Forces must form a closed polygon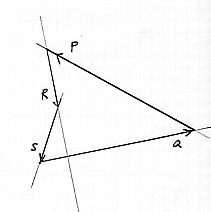

From http://www.ecf.toronto.edu/apsc/courses/civ214/Lectures/Equilibrium%20of%20coincident%20forces.html

! Beware of Parallel Forces...

There is one situation when you can have equilibrium, three forces, but they are not concurrent. Parallel forces!
For example, in this screw clamp below the wooden jaws are under 3 forces. They are parallel so they cannot intersect. They must still balance of course, or the clamp will not be in equilibrium (which means it must be accelerating). To analyse the wooden jaw, this type of problem falls into the non-concurrent force category which we will study later.

Whiteboard:

Whiteboard

Questions:

Three Force Questions.pdf (Ivanoff old edition)

Homework Assignment:
Do questions 4:9 to 4:20. (New book 5:9 to 5:20)
Draw the Space Diagram, Free Body Diagram and Force Polygon for each question.
You can use CAD (recommended for the FBD) and/or Excel. (Or you can do it mathematically by hand if you really want to!).
Note: Excel is not permitted during this test (Tester: Exam mode).